
By training this particular CNN given external dataset, we can refine the resulting transform and boost its performance. We focus specifically on the DCT denoiser Īnd show that it can be seen as a shallow CNN with weights corresponding to the DCT projection kernel and a hard shrinkage function as activation function. Our work contributes to the recent trend, which builds on traditional algorithms and revisits them with a dose of deep learning, while keeping the original intuition. Most of those methods achieved state-of-the-art results until recently. By gathering together the most similar patches and denoising them all at once, considerable gains in performance can be obtained. Indeed, it was observed that, within the same image, similar patches are repeated in the whole image. In the meantime, the N(on)L(ocal)-means algorithm opened the door to a new category of denoising algorithms exploiting the self-similarity assumption. An improvement of such methods consists in considering an overcomplete dictionary instead, under an assumption of sparse representation: each patch of an image is supposed to be sufficiently represented by a few vectors of an overcomplete basis. , has the advantage to be both simple and fast but also the drawback of suppressing fine details in the image. This strategy, coming from compression algorithms Frequency-based methods, aiming at decomposing the signal in a DCT or wavelet basis and then shrinking some transform coefficients, were considered quite early. Over the years, a rich variety of methods have been proposed to deal with this issue with inspiration coming from multiple fields. Experiments onĪrtificially noisy images demonstrate that two-layer DCT2net providesĬomparable results to BM3D and is as fast as DnCNN algorithm composed of more Image patches while DCT is optimal for piecewise smooth patches. That these two methods can offer DCT2net is selected to process non-stationary Original hybrid solution between DCT and DCT2net is proposed combining the best To deal with remaining artifacts induced by DCT2net, an This gives birth to a fully interpretable CNNĬalled DCT2net.
In this paper, we demonstrate that a DCTĭenoiser can be seen as a shallow CNN and thereby its original linear transformĬan be tuned through gradient descent in a supervised manner, improvingĬonsiderably its performance. Networks (CNN) have outperformed their traditional counterparts, making signal Since a few years however, deep convolutional neural Still used in crucial parts of state-of-the-art "traditional" denoisingĪlgorithms such as BM3D.
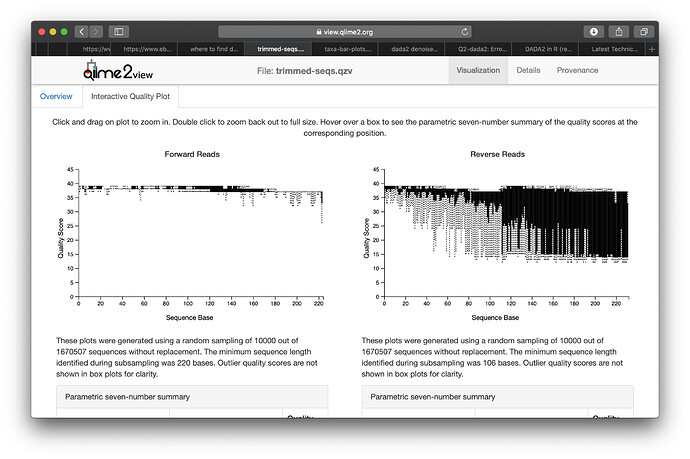
Processing, has been well studied over the years. Well-known DCT image denoising algorithm. This work tackles the issue of noise removal from images, focusing on the


 0 kommentar(er)
0 kommentar(er)
